Matrice somma prodotto

Nell’ambito dell’utilizzo delle matrici nelle formule e funzioni, introduciamo in questa sede una funzione matriciale che si trova nell’ambito delle funzioni matematiche: MATR.SOMMA.PRODOTTO.
Come prima cosa, scomponiamo il suo nome nelle varie parti che lo costituiscono, per comprenderla al meglio.

• MATR. sta per “Matrice” ovvero un intervallo di celle che si sviluppa in entrambe le dimensioni ovvero in altezza (colonne) e larghezza (righe). Ad esempio, A2:C80 è una matrice.

• SOMMA è, ovviamente, la funzione che somma tutti i valori presenti in un intervallo.

• PRODOTTO è il risultato di una moltiplicazione dei valori.

Nella sua accezione letterale, la funzione MATR.SOMMA.PRODOTTO calcola in un colpo solo il prodotto di una serie di valori disposti in una matrice e ne effettua la somma.
Di fatto, serve per avere in un colpo solo il risultato della somma di una serie di valori che vanno moltiplicati tra di loro. Un esempio può chiarirne il funzionamento più di mille parole.
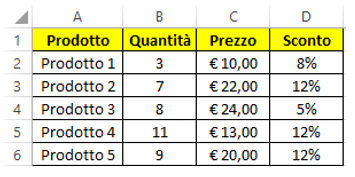
Nell’immagine sotto si possono vedere alcune righe di un prospetto dove sono presenti, per ogni prodotto preso in esame, le quantità, il prezzo unitario ed una percentuale di sconto.
Senza calcolare il prezzo scontato per ogni prodotto, si vuole conoscere il prezzo scontato complessivo per tutto l’ordine.



Invece di fare altre colonne, si possono usare due funzioni MATR.SOMMA.PRODOTTO e collocare i risutati in due celle diverse, una che somma il prodotto di tutte le quantità vendute ed una che somma lo sconto del prodotto tra quantità, prezzo e sconto.
Infatti, i soli argomenti della funzione MATR.SOMMA.PRODOTTO sono i vari intervalli o matrici, separate da punto e virgola.
La sua sintassi è, infatti, la seguente: =MATR.SOMMA.PRODOTTO(matrice1; matrice2; …).
Appurato che la matrice delle quantità è B2:B23, quella dei prezzi unitari è C2:C23 e quella degli sconti è D2:D23, le funzioni separate sono le seguenti:

• =MATR.SOMMA.PRODOTTO(B2:B23;C2:C23) calcola la somma complessiva dell’ordine. Come si vede gli argomenti sono due ovvero le due matrici (matrice 1 e matrice 2).

• =MATR.SOMMA.PRODOTTO(B2:B23;C2:C23;D2:D23) calcola la somma complessive dello sconto da sottrarre al risultato precedente ovvero al totale dell’ordine. In questo caso è usato anche il terzo argomento (matrice 2).

Nell’esempio, si è voluto immettere due funzioni in due celle diverse e poi calcolare la differenza in una terza cella, ma nulla vieta di inserire le funzioni in una cella sola.
Ciò che ne risulta sarà: =MATR.SOMMA.PRODOTTO(B2:B23;C2:C23)- MATR.SOMMA.PRODOTTO(B2:B23;C2:C23;D2:D23).
L’uso della funzione MATR.SOMMA.PRODOTTO in luogo dell’inserimento di colonne aggiuntive in cui calrolare le singole formule per poi farne la somma può facilitare le operazioni, ma non serve ancora ad illustrare le potenzialità di tale funzione in questa newsletter che rappresenta, come detto inizialmente, solo una introduzione, prima di vedere in un’altra occasione due o tre possibili campi di utilizzo avanzati, in cui essa diventa fondamentale.
Ciò vale anche per un secondo uso che se ne può fare, in luogo delle funzioni di calcolo a più condizioni ovvero CONTA.PIÙ.SE e SOMMA.PIÙ.SE.
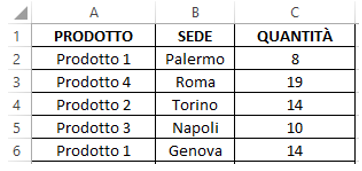
Si veda l’esempio sottostante, in cui si ripetono le vendite di prodotti differenti in differenti sedi.
Si vuole sapere quante volte il Prodotto5 è stato venduto a Palermo e le quantità che ne sono state vendute.
I criteri o condizioni sono due: il prodotto deve essere il Prodotto5 e la sede di vendita deve essere Palermo.



Anche in questa circostanza può essere utile ricorrere alla funzione MATR.SOMMA.PRODOTTO, se non altro perché può avere per molti una sintassi un pochino più semplice rispetto alle funzioni di calcolo condizionale.
Il problema che sorge è che, rispetto al primo esempio, le celle delle matrici non contengono solo numeri ma anche testi.
Nel caso di testi, la funzione restituisce VERO o FALSO a seconda che la cella rispetti o meno la condizione posta.
Con una piccola accortezza, si può fare in modo che VERO restituisca il valore 1 e FALSO il valore 0 cosicché possano essere sottoposti a calcoli.
L’accortezza è mettere un doppio segno meno (--) davanti alle matrici, che a quel punto dovranno essere poste tra parentesi.
Nel caso dell’esempio, sapendo che l’intervallo dei prodotti è A2:A27, quello delle sedi B2:B27 e quello delle quantità vendute C2:C27 e che i criteri (Prodotto5 e Palermo) sono stati digitati rispettivamente nelle celle I2 e J2, la funzione che conta quante volte il prodotto 5 è stato venduto a Palermo è la seguente: =MATR.SOMMA.PRODOTTO(--(A2:A27=I2);--(B2:B27=J2)).
Come si vede le due matrici sono precedute dal doppio segno meno e viene verificato quanto il contenuto è uguale a quello che c’è nella cella I2 nel primo caso (Prodotto5) e J2 nel secondo caso (Palermo). Per sommare le quantità vendute a Palermo del Prodotto 5, basta aggiungere come terza matrice C2:C27, in questo caso senza doppio segno meno poiché contiene numeri.
La funzione risultante è: =MATR.SOMMA.PRODOTTO(--(A2:A27=I2);--(B2:B27=J2);C2:C27).
Ora conosciamo la funzione e prossimamente ne vedremo campi di utilizzo più affascinanti!